문제 : https://www.acmicpc.net/problem/4948
4948번: 베르트랑 공준
베르트랑 공준은 임의의 자연수 n에 대하여, n보다 크고, 2n보다 작거나 같은 소수는 적어도 하나 존재한다는 내용을 담고 있다. 이 명제는 조제프 베르트랑이 1845년에 추측했고, 파프누티 체비쇼
www.acmicpc.net
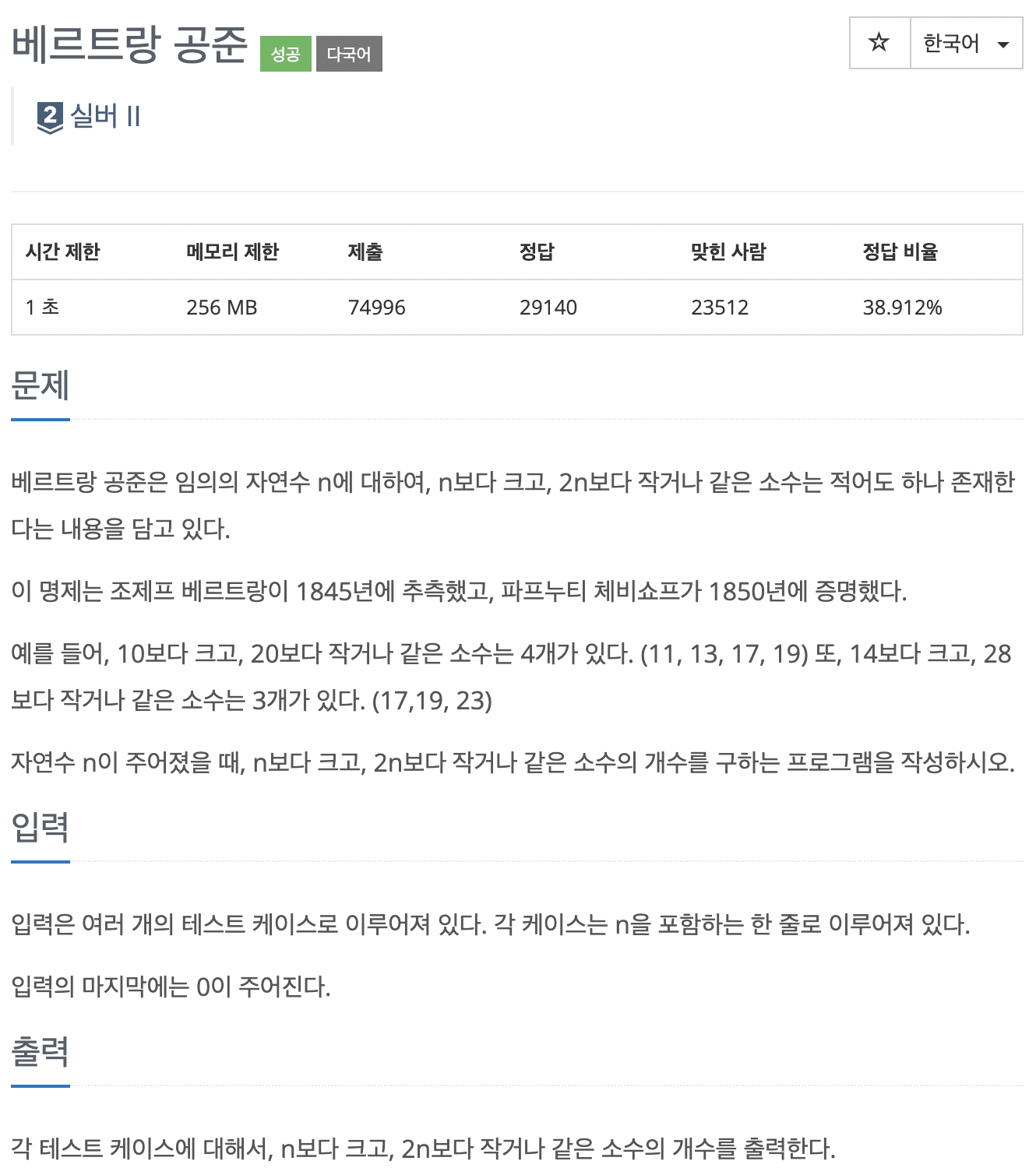
어떤 문제인가?
베르트랑과 채비 쇼프라는 분께서 만드신 명제를 구현하는 것이다.
입력한 수 n에 대해 n초과~2n이하의 범위에 존재하는 소수의 개수를 출력하면 된다.
접근 방법
여기서 에라토스테네스의 체라는 개념이 사용된다.
에라토스테네스의 체에 대해 모른다면 이해가 안 될 것이니 보는 것을 추천한다.
bool arr[123456 * 2 + 1];
for (int i = 2; i <= 123456 * 2; i++) {
arr[i] = true;
}
for (int i = 2; i * i <= 123456 * 2; i++) {
if (!arr[i]) {
continue;
}
for (int j = i * i; j <= 123456 * 2; j += i) {
arr[j] = false;
}
}이 부분이 에라토스테네스의 체를 구현한 코드이다.
n이 123,456까지 입력될 수 있으니 2n까지인 123,456*2 + 1개를 저장할 배열을 선언한다.
에라토스테네스의 체에 대한 이해가 있다면 코드는 바로 이해가 될 것이므로 따로 설명하지 않겠다.
int n;
while (true) {
cin >> n;
int cnt = 0;
if (n == 0) {
break;
}
for (int i = n + 1; i <= 2 * n; i++) {
if (arr[i]) {
cnt++;
}
}
cout << cnt << "\n";
}이 부분이 n초과 2n이하 범위의 소수의 개수를 출력하는 부분이다.
n이 0일 때 반복문을 탈출해서 끝이 난다.
for문을 돌며 배열의 n+1번 인덱스부터 2n번 인덱스까지 순회하며
배열의 인덱스 값이 참이라면 cnt를 증가시켜준다.
마지막으로 cnt를 출력하면 끝!!
무엇이 어려웠는가?
사실 나도 에라토스테네스의 체에 대해 이번에 처음 알게 되었다.
그래서 에라토스테네스의 체를 구현하는 것이 약간 어렵게 느껴졌던 것 같다.
그 외에는 단순한 구현 문제라 특별히 어려운 부분이 없었다.
배운 점
수학은 참 대단하다.
사실 처음에는 에라토스테네스의 체를 사용하지 않고
각 수를 2부터 sqrt(x)까지 순회하며 직접 소수의 개수를 구하는 방법을 사용했는데 당연히 시간초과가 발생했다.
수학적인 개념을 사용해서 선형시간을 상수시간으로 단축할 수 있다는 것이 신기했다.
수학을 잘하지 못하는데 수학의 중요성을 다시금 느낄 수 있었다.
'백준 문제풀이(BOJ PS)' 카테고리의 다른 글
| [백준(BOJ)] 3036번 링 C++ (0) | 2022.08.02 |
|---|---|
| [백준(BOJ)]골드바흐의 추측(에라토스테네스의 체) C++ (0) | 2022.08.01 |
| [백준(BOJ)] 5052번 전화번호 목록 C++ (0) | 2022.07.27 |
| [백준(BOJ)] 9935번 문자열 폭발 C++ (0) | 2022.07.27 |
| [백준(BOJ)] 19638번 센티와 마법의 뿅망치 C++ (0) | 2022.07.27 |
